Colorizing Prokudin-Gorskii

Overview

The goal of this project is to automatically reconstruct color photographs from the filtered glass plate negatives of Sergei Mikhailovich Prokudin-Gorskii, an early 20th century photographer. Each negative contains three separate exposures of images taken through blue, green, and red filters (from top to bottom). Since I need to stitch these components together, the primary challenge of this project is calculating how each exposure is displaced to correctly align each color filter. Later, I extend on this algorithm with some optimizations, color correction, and cropping in postprocessing.

Input and preprocessing

Emir of Bukhara (1911), sample original glass plate (blue, green, red from top to bottom)

Before running our alignment algorithms, we simply divide the raw digitzed negative into thirds, since this approximately correctly divides each color filter into their respective color filter category.

Blue, green, red, respectively

Part 1: Alignment Metrics

My first approach focusses on minimizing the L2 Norm between a reference filter (green) to the other two filters. This metric simply evaluates the aggregate Euclidean distance between the reference and the target filter, which generally works well, but is highly sensitive to brightness differences between channels (i.e., matching based on the Emir’s robe above is not great for L2).

My second approach focusses on maximizing normalized cross-correlation (NCC), which is more robust, since it is invariant to linear changes in brightness and contrast. This method was generally more effective, since different color filters produce varying intensities.

L2 Norm

\[E(\Delta x, \Delta y) = \sum_{x,y} \Big( R(x,y) - F(x+\Delta x, y+\Delta y) \Big)^2\]

We minimize $E(\Delta x, \Delta y)$ to find the displacement $(\Delta x, \Delta y)$ where the shifted filter $F$ best overlaps with the reference $R$.

Normalized Cross-Correlation (NCC)

\[\text{NCC}(\Delta x, \Delta y) = \frac{\sum_{x,y} \big(R(x,y) - \bar{R}\big)\big(F(x+\Delta x, y+\Delta y) - \bar{F}\big)} {\sqrt{\sum_{x,y} \big(R(x,y) - \bar{R}\big)^2} \, \sqrt{\sum_{x,y} \big(F(x+\Delta x, y+\Delta y) - \bar{F}\big)^2}}\]

We maximize $\text{NCC}(\Delta x, \Delta y)$ to find the displacement that yields the strongest correlation between $R$ and $F$, regardless of brightness or contrast differences.

$R(x,y)$: Reference filter/channel (kept fixed, e.g. green).
$F(x+\Delta x, y+\Delta y)$: Filter/channel being aligned (shifted version of red or blue).
$(\Delta x, \Delta y)$: Displacement vector we are solving for.
$\bar{R}, \bar{F}$: Mean pixel intensities of $R$ and $F$, used for normalization in NCC.

Small Image Examples

Here are some first outputs I achieved with these two approaches.

Monastery, L2 Norm

NCC

Tobolsk, L2 Norm

NCC

Cathedral, L2 Norm

NCC

Below are the filter displacements found by both approaches.

Image Name	L2 Blue Displacement	L2 Green Displacement	L2 Red Displacement	NCC Blue Displacement	NCC Green Displacement	NCC Red Displacement
monastery	(3, -2)	(0, 0)	(6, 1)	(3, -2)	(0, 0)	(6, 1)
tobolsk	(-3, -3)	(0, 0)	(4, 1)	(-3, -3)	(0, 0)	(4, 1)
cathedral	(-5, -2)	(0, 0)	(7, 1)	(-5, -2)	(0, 0)	(7, 1)

Part 3: Coarse-to-Fine Pyramid Search

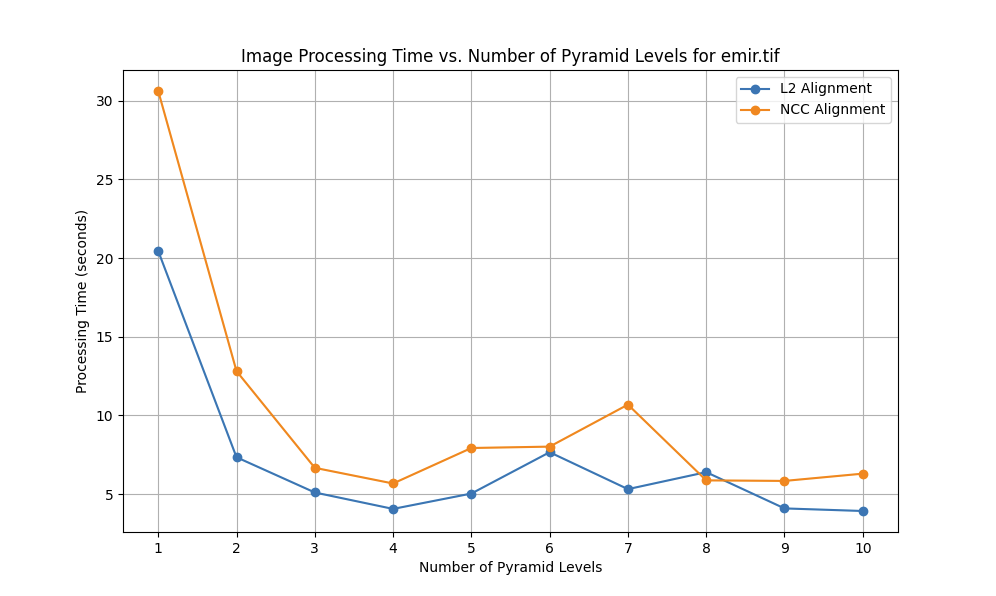
The next challenge is that searching for the correct alignment on large images by checking every possible shift is too slow. To speed this up, I use an image pyramid. This approach starts by finding a rough alignment on a small, downscaled version of the image, which is very fast. This rough alignment is then used to guide a more focused search on a larger, higher-resolution version. By repeating this process from coarse to fine, I can quickly and accurately align the full-resolution image, even when the initial misalignment is large.

The process begins by applying a Gaussian blur with $\sigma = 1$ to the image. This is an anti-aliasing filter to reduce artifacts when the image is downscaled. I use a rescaling factor of 0.5, meaning each level of the pyramid is half the width and height of the one above it, and all larger images in the dataset are constructed with 4 levels. The alignment starts at the smallest scale, performing a search within a +/- 15 pixel displacement range in both x and y to find a coarse alignment. This calculated displacement is then doubled and propagated to the next higher-resolution level, where it is used to shift the image. A search with a smaller displacement range of +/- 2 pixels then refines the alignment. This process of scaling the displacement and performing a fine-tuned local search is repeated until the original, full-resolution image is reached.

Pyramid Search Time Optimization

Time complexity comparison showing the speed improvement of pyramid search across levels with abovementioned hyperparameters. Level 2 onwards converges to an accurate displacement result.

Full Gallery

Church, L2 Norm

NCC

Emir, L2 Norm

NCC

Harvesters, L2 Norm

NCC

Icon, L2 Norm

NCC

Italil, L2 Norm

NCC

Lastochikino, L2 Norm

NCC

Lugano, L2 Norm

NCC

Melons, L2 Norm

NCC

Self Portrait, L2 Norm

NCC

Siren, L2 Norm

NCC

Three Generations, L2 Norm

NCC

Below are the filter displacements found by both approaches.

Image Name	L2 Blue Displacement	L2 Green Displacement	L2 Red Displacement	NCC Blue Displacement	NCC Green Displacement	NCC Red Displacement
emir	(-49, -24)	(0, 0)	(57, 17)	(-49, -24)	(0, 0)	(57, 17)
italil	(-38, -21)	(0, 0)	(39, 15)	(-38, -21)	(0, 0)	(39, 15)
church	(-25, -4)	(0, 0)	(33, -8)	(-25, -4)	(0, 0)	(33, -8)
three_generations	(-53, -14)	(0, 0)	(59, -3)	(-53, -14)	(0, 0)	(59, -3)
lugano	(-41, 16)	(0, 0)	(53, -13)	(-41, 16)	(0, 0)	(52, -13)
melons	(-82, -11)	(0, 0)	(96, 3)	(-82, -11)	(0, 0)	(96, 3)
lastochikino	(3, 2)	(0, 0)	(78, -7)	(3, 2)	(0, 0)	(78, -7)
icon	(-41, -17)	(0, 0)	(48, 5)	(-41, -17)	(0, 0)	(48, 5)
siren	(-50, 6)	(0, 0)	(47, -19)	(-49, 6)	(0, 0)	(47, -19)
self_portrait	(-79, -29)	(0, 0)	(98, 8)	(-79, -29)	(0, 0)	(98, 8)
harvesters	(-59, -17)	(0, 0)	(65, -3)	(-59, -17)	(0, 0)	(65, -3)

Bells & Whistles

Automatic Contrast

From these results, I wanted to extend on the project, by improving the contrast in an image by spreading out the most frequent intensity values. I achieved this by equalizing the histograms of all three color filters, making the distribution of pixel intensities more uniform.

Histogram equalization works by transforming the pixel intensities based on their own distribution. First, a histogram of the image’s pixel intensities is computed, which is used to calculate the CDF (the cumulative sum of pixel counts up to each intensity level). The CDF is normalized, creating a transfer function that maps the original intensity values to a new range. Each pixel’s intensity in the original image is then replaced by its corresponding value from the normalized CDF. This remapping effectively spreads out the most frequent intensity values, stretching the distribution across the full dynamic range.

Automatic Cropping

To eliminate the discolored border artifacts created by the channel alignment process, I apply an automatic cropping procedure to the final colorized image. This method simply removes a 5% margin from all edges of the image, resulting in a cleaner final output.